Location: Computing Department, Goldsmiths, University of London (UK).

Supervisor: Prof. Mark Bishop.

Abstract

Stochastic Diffusion Search (SDS) is a swarm intelligence heuristic providing a population-based solution to the exploration/exploitation dilemma. SDS agents perform cheap, partial evaluations of candidate solutions (test phase) before sharing information about their hypotheses through direct one-to-one communication (diffusion phase). The repetition of these two phases leads to the emergence of high-quality solutions identifiable in clusters of agents sharing the same hypotheses.

In Stochastic Diffusion Search applied to Trees (SDST), a meta-population of agents explores a game-tree in a Monte-Carlo Tree Search style, ultimately converging to the optimal solution. Each node of the game-tree is solved through a standard application of SDS, but the convergence of the root node population is coupled to the convergence of populations down the game-tree. SDST agents also have a natural tendency to descend in the population pointed by their hypothesis and they spontaneously move upward when they are not contacted by other agents.

These simple rules result in complex dynamics characterized by a meta-level of swarm behaviour (a swarm of populations or a meta-population). One can think of this two-leveled distributed system as a loose metaphor for the hierarchical organization of the brain, from neurons and cortical columns to Brodmann areas and cerebral lobes.

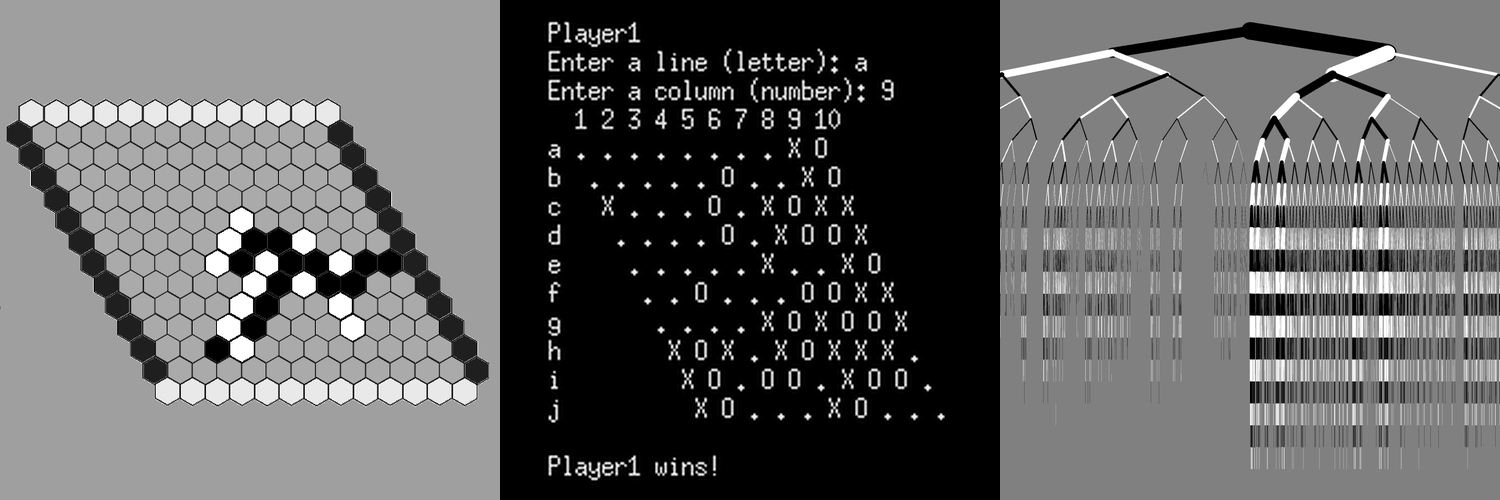
Animation

In the animation above, SDST is applied to a binary game tree of depth 20 designed such that:

  • If Black moves Right, most of the possible outcomes (90%) are favorable to Black.
  • If Black moves Left, most of the possible outcomes (90%) are favorable to White.

However:

  • If Black moves Right, there exists a winning strategy for White.
  • If Black moves Left, there exists a winning strategy for Black.

Solving this game-tree requires good tactical play: moving Right is statistically better for Black, but moving Left is the only guaranteed path to victory.

The width of each branch in the animation is proportional to the number of agents in the parent node population supporting the move leading to the child node population. Initially, most of the agents are allocated to the exploration of the Right part of the game tree. This lasts until the winning strategy for White is found (always playing Left) and the agents then shift to the exploration of the Left part of the game tree. At the end, the winning strategy for Black is found (always playing Left). The fact that all the agents in the root node population converge to the Left move indicates that Black should play Left.

(coded in C++, animated using openFrameworks)

More

Tanay, T., Bishop, J. M., Nasuto, S. J., Roesch, E. B., & Spencer, M. C. (2013). Stochastic diffusion search applied to trees: a swarm intelligence heuristic performing monte-carlo tree search. In Proceedings of the AISB.

Tanay, T. (2012). Game-Tree Exploration using Stochastic Diffusion Search (Master’s thesis).