GRVS: a Generalizable and Recurrent Approach to Monocular Dynamic View Synthesis

arXiv 2025

*equal contribution

Huawei Noah’s Ark Lab

Abstract

Synthesizing novel views from monocular videos of dynamic scenes remains a challenging problem. Scene-specific methods that optimize 4D representations with explicit motion priors often break down in highly dynamic regions where multi-view information is hard to exploit. Diffusion-based approaches that integrate camera controls into large pre-trained models can produce visually plausible videos but frequently suffer from geometric inconsistencies across both static and dynamic areas. Both families of methods also require substantial computational resources.

Building on the success of generalizable models for static novel view synthesis, we adapt the framework to dynamic inputs and propose a new model with two key components: (1) a recurrent loop that enables unbounded and asynchronous mapping between input and target videos and (2) an efficient use of plane sweeps over dynamic inputs to disentangle camera and scene motion, and achieve fine-grained, six-degrees-of-freedom camera controls. We train and evaluate our model on the UCSD dataset and on Kubric-4D-dyn, a new monocular dynamic dataset featuring longer, higher resolution sequences with more complex scene dynamics than existing alternatives.

Our model outperforms three Gaussian Splatting-based scene-specific approaches, as well as two diffusion-based approaches in reconstructing fine-grained geometric details across both static and dynamic regions.

Method

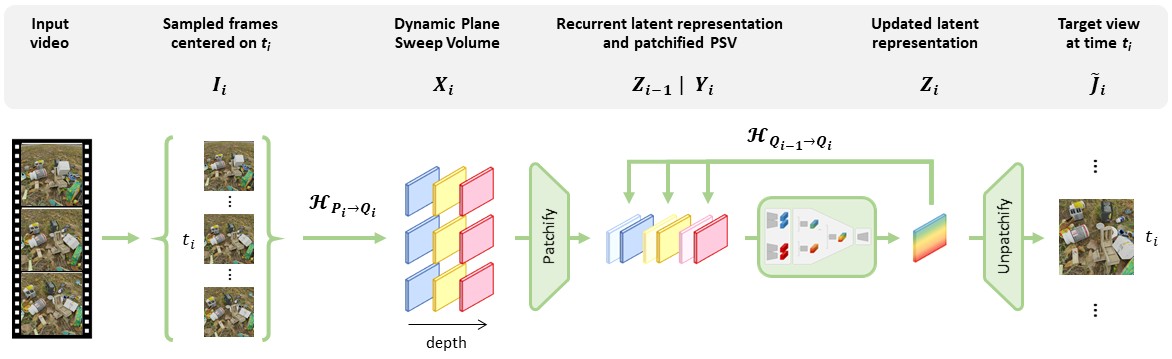
Overview of GRVS. For a target view $\mathbf{J}_{i}$ at time $t_i$ and with camera parameters $\mathbf{Q}_{i}\,$, our Generalizable Recurrent View Synthesizer consists of 5 stages. 1) The selection of $V$ input views $\mathbf{I}_{i}$ uniformly sampled around the time $t_i\,$, with corresponding camera parameters $\mathbf{P}_{i}$. 2) The projection of $\mathbf{I}_{i}$ into a dynamic plane sweep volume $\mathbf{X}_{i}$ using the homographies $\mathcal{H}_{\mathbf{P}_{i} \to \mathbf{Q}_{i}}$. 3) The patchification and reshaping of $\mathbf{X}_{i}$ into a downsampled tensor $\mathbf{Y}_{i}$. 4) The latent rendering of $\mathbf{Y}_{i}$ into a hidden state $\mathbf{Z}_{i}$ using the recurrent hidden state $\mathbf{Z}_{i-1}$ projected using the homographies $\mathcal{H}_{\mathbf{Q}_{i-1} \to \mathbf{Q}_{i}}$. 5) The decoding of $\mathbf{Z}_{i}$ into the predicted output $\mathbf{\tilde{J}}_{i}$.

Video Results

UCSD

We compare our model to three recent methods based on Gaussian Splatting (GS) for monocular dynamic novel view synthesis: D-3DGS, SC-GS and 4DGS. Given a synthetic monocular sequence generated as described in the main paper, we freeze the time mid-sequence and move the camera following a spiral trajectory. We also show some input frames before and after the spiral for clarity. 4DGS, D-3DGS and SC-GS struggle on this task, especially on dynamic regions but also to a lesser extent on static regions, because of the sparse nature of the synthetic sequences used, where only 10 distinct viewpoints are available throughout the sequences (since there are only 10 static cameras). In comparison, our approach performs remarkably well.

Kubric-4D-dyn with spiral trajectories

We now compare our model to the same three baselines on the Kubric-4D-dyn dataset. Again, given a synthetic monocular sequence generated as described in the main paper, we freeze the time mid-sequence and move the camera following a spiral trajectory. We also show the input sequence before and after the spiral for clarity. The baselines now reconstruct the static regions well, but they still struggle on the dynamic regions. In comparison, our approach is able to reconstruct both static and dynamic elements with high accuracy.

Kubric-4D-dyn with gradual trajectories

We now compare our model to two Diffusion-based approaches: GCD and Gen3C. In this scenario, the output camera starts at the same position as the input camera in the first frame, and linearly progresses toward a certain target position reached at the last frame. The time in the output is synchronized with the input. This choice was motivated by the fact that the best performing model of GCD was trained on these types of output sequences on a Kubric variant. The output video size is based on the capacity of GCD, that can only output 14 frames with a single diffusion sample. All three methods perform reasonably well, but our method reconstructs fine-grained geometric details much more accurately.

Out of distribution videos (DAVIS)

Finally, we show output videos generated by our model on in-the-wild sequences from the DAVIS dataset. The distribution of these sequences is relatively far from the distribution of the sequences used during training. The UCSD sequences consist of ``teleporting" virtual cameras moving at high velocity, only sampling a very sparse set of viewpoints (10 physical cameras). The Kubric sequences consist of rigid objects sampled from a relatively small set and disposed on a flat surface. Nonetheless, our model generalizes well to these out-of-distribution sequences.

Ablation

Here, we compare the effect of turning on and off the recurrent connection when generating the spiral trajectories from the previous sequences. At the top, the recurrent connection is off. At the bottom, the recurrent connection in on. As expected, the recurrent connection significantly improves the perceptual quality and temporal consistency of the results.